Il Mulino del Tempo: Mezzo schema di Marino di Tiro

Il nostro pianeta va visto come una sfera. La sfera si può misurare, oggi, con una certa facilità grazie agli studi di Archimede. Per quello che ci riguarda dobbiamo mettere a fuoco, bene, il concetto del grande cerchio che è l’Equatore e la sua misura di 40.076 Km. Altri grandi cerchi sono i singoli meridiani (comprensivi degli antimeridiani) che passano per i Poli.

Nulla ci vieta di immaginare un grande cerchio che possiamo far passare, dove ci serve, sopra la sfera. Immaginiamo di segnare due punti in qualsiasi parte della superficie della sfera. Su quei due punti possiamo far passare un grande cerchio. La parte del nuovo grande cerchio, che tocca i due punti segnati della sfera, è la parte che ci permette di misurare la distanza tra le due località. Il nuovo grande cerchio è identico a quello dell’Equatore. Basta misurare, con l’apertura delle punte di un compasso, le due località segnate e vedere a quale lunghezza (quanti gradi) corrisponde rispetto all’Equatore. Se si conosce la misura dell’Equatore non ci sono problemi. Se non si conosce questa misura bisognerebbe ricavarla. Se io fossi stato un Egiziano, di quelli antichi, sapendo che il Tropico cade a 24° e la Grande Piramide è a 30°… avrei misurato accuratamente la distanza di quei 6° sul meridiano della Piramide e lo avrei moltiplicato per 60. (6 x 60 = 360). In Egitto c’erano degli abili tenditori di corde che non facevano altro che misurare tutto il paese. Un certo Eratostene, per non far capire che aveva ricopiato il metodo egiziano, lo ha personalizzato e spacciato per una sua grande scoperta. Così va il Mondo. Torniamo alla distanza minima tra due località e alla linea immaginaria che le collega: quella linea segue la curvatura della sfera. A quali calcoli complicatissimi bisogna far ricorso per conoscere la distanza delle due località?

Ma vi sembra mai possibile che Marino di Tiro non ci sia venuto incontro? Con lo schema RoBer si fa di tutto. Con l’Organum Directorium si possono disegnare gli schemi nelle diverse scale..

… e si può fare altro?

Ho visto che Mercatore ha raffigurato una strana proiezione e un suo Organum Directorium.

Da quella proiezione, con lo schema RoBer, posso ottenere (partendo dall’Equatore) il Tropico, il 32° ( o il parallelo di Alessandria?), il 50°, il 60°, il Circolo Polare, e il 70° e il 75° parallelo. Precisi precisi. Completare la scala non è difficile. Ma a cosa serve quella strana proiezione che, con la proiezione cilindrica modificata di Mercatore, non c’entra assolutamente nulla?

A questo punto ho voluto vederci chiaro.

L’Equatore misura 40.076 Km. L’ho semplificato in 40.000. Ogni 90° di Equatore sarebbero pari a 10.000 Km. Ogni 9° sarebbero 1.000 Km e ogni 4,5° sarebbero 500 Km.

Non solo sull’Equatore perchè ho assegnato queste distanze al meridiano ultimo, a sinistra, del quadrato che delimita l’Organum Directorium rispettando la corrispondenza dei singoli 9 gradi di parallelo. Se si proietta un –meridiano- allora anche i settori in kilometri risulteranno proiettati proporzionalmente. Ho portato queste misure sull’Organum Directorium.

Così ci spiegano Mercatore:

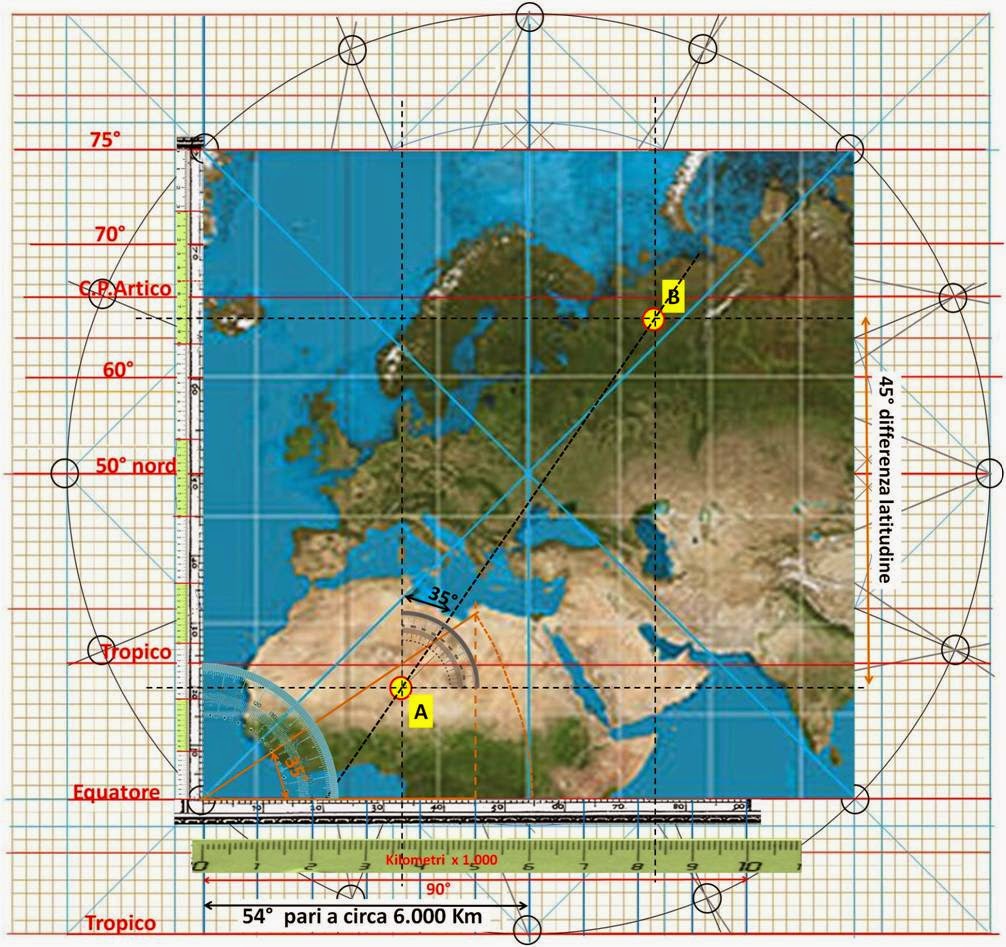
Il meridiano Zero è quello delle Azzorre. La prima località, per capire l’esempio,è posta a 20° nord e a 33° a est dalle Azzorre. La seconda località è posta a 65° nord e a 75° a est delle Azzorre. La differenza tra le due latitudini è di 45°. Molto curiosa l’impostazione! Gli Autori hanno fatto, solo, un esempio oppure, quelle particolari coordinate sono, in qualche altro scritto del Mercatore?

In attesa di chiarimenti vado avanti. La retta che attraversa le località A e B cade con una certa incidenza sull’Equatore: Angolo interno 55° mentre l’esterno è di 35° (+90°).

A questo punto si parte con i due goniometri dell’organum directorium.

Si invertono i valori dell’angolo di incidenza (perché?). Si riporta il tutto sul meridiano zero. Da quel meridiano si calcolano i 45° di differenza di latitudine e si tira una retta che va ad intercettare la nuova retta incidente (color arancione). Poi con un compasso si traccia un arco di circonferenza dove c’è il contatto con l’Equatore, sono 54°; e si fa il calcolo della distanza. E questo dovrebbe essere, anche, il pensiero di Mercatore.

Gli autori, ricorrendo anche alla moderna matematica, con una bellissima formula spiegano il tutto.

Io resto perplesso. Guardo e riguardo lo schema e

… ma non è più semplice fare questo passaggio?

Tracciamo la retta che attraversa le due località (ortodromica). Da dove questa retta tocca l’Equatore si dovrebbero far partire i 45° di differenza di latitudine. Dopo i 45° si dovrebbe tirare la retta che attraverserà nel punto X l’ortodromica. Siamo a 58° nord. Il tratto A-X dà l’esatto valore reale dell’ortodromica; riportandolo sull’Equatore: come ha già evidenziato una delle diagonali.

Io uso settori da 4,5° e 9°. In 90° riporto 10 settori da 9°. Ma a 45° e 90° i metodi si sincronizzano.

90° sono 90°. Ogni 9° sono 1.000 Km. 90° sono 10.000Km.

Qualcuno sa spiegarmi cosa c’entra la Rosa dei Venti e l’Organum Directorium in tutto questo discorso?

Anticamente, quando tutto ruotava attorno ad Alessandria, questo schema,bastava ed avanzava. Abbiamo visto come si passava da una scala all’altra. Adesso abbiamo tutta la sfera della Terra.

Come si operava? Vi spiego qualche piccolo trucco.

Impostate, con la massima precisione il Quadrato di gradi 108° (12 settori da 9 gradi) all’Equatore.

Come dice L’Organum Directorium disegniamo i 75° con quel particolare sviluppo che nasce con gli schemi dei Portolani. Tracciamo le due diagonali e il meridiano centrale. Facciamo la prima verifica. Andremo a misurare il tratto Londra Cuba dopo aver preso la distanza con Google Maps.

Si selezionano le due località da misurare. Dobbiamo trovare con la massima precisione il centro tra le due località. Una volta trovato il centro preciso si mettono 54° a destra e 54° a sinistra (sono 108° precisi). Si prende la distanza della differenza di latitudine 23° nord e 51° nord, che rende 28 gradi, e la si duplica. Si traccia una nuova retta da Cuba che va a toccare la estremità la duplicazione della differenza di latitudine. Dove questa retta tocca l’Equatore … segna direttamente la distanza.

(Non sperate che ve la spieghi matematicamente …. )

C’è un altro metodo:

Noi abbiamo uno sviluppo di paralleli; particolare ed unico. Se prendiamo direttamente la differenza di latitudine da questo sviluppo, vedasi la scala in gradi di sinistra, dobbiamo impostare sul lato destro una scala lineare di 108° come quella dell’Equatore. Misuriamo la differenza di latitudine a sinistra: Siamo a 23° nord e 51° nord. Differenza di latitudine di 28° . Simulando che il lato destro sia l’Equatore … prendiamo i 28° lineari. Tracciamo la retta (rossa) e il punto di contatto dà la distanza.